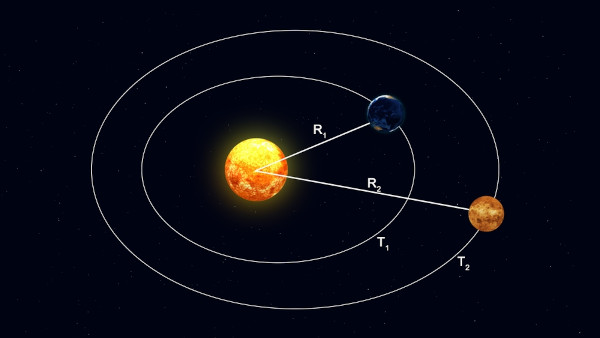
A terceira lei de Kepler é uma lei que diz que o quadrado do período de revolução de um corpo celeste é diretamente proporcional ao cubo do raio médio da sua órbita ao redor de outro corpo celeste. Por isso, quanto mais perto estivermos de outro corpo celeste, menor será o tempo de translação e menor será a distância entre os corpos.
Leia também: O que diz a primeira lei de Kepler?
Tópicos deste artigo
- 1 - Resumo sobre a terceira lei de Kepler
- 2 - O que diz a terceira lei de Kepler?
- 3 - Fórmula da terceira lei de Kepler
- 4 - Aplicação da terceira Lei de Kepler
- 5 - Exercícios resolvidos sobre terceira lei de Kepler
Resumo sobre a terceira lei de Kepler
- A terceira lei de Kepler é a lei formulada por Johannes Kepler para relacionar a distância e o período de revolução de um corpo celeste em torno de outro.
- Foi formulada por Johannes Kepler entre 1609 e 1619.
- É descrita pela razão entre o cubo do raio médio da órbita do corpo celeste e o quadrado do período de revolução do corpo celeste.
- É aplicada na astronomia e astrofísica.
O que diz a terceira lei de Kepler?
Formulada por Johannes Kepler, a terceira lei de Kepler, nomeada como lei dos períodos ou lei harmônica, é enunciada como:
“O quadrado do período de qualquer planeta é proporcional ao cubo do semieixo maior da órbita.”
Isso significa que se o tempo de revolução (translação) de um corpo celeste ao redor de outro é maior, então maior será a distância entre eles e maior será o tempo para que o primeiro complete uma volta no segundo.
Essa lei foi criada pelo astrônomo, astrólogo e matemático Johannes Kepler (1571-1630) com o intuito de obter a relação entre a distância e o período de revolução de um corpo em torno do Sol (ou outro corpo celeste).
Fórmula da terceira lei de Kepler
A fórmula que descreve a terceira lei de Kepler é:
\(\frac{T^2}{R^3} = \text{constante} \)
- T → período de revolução, ou seja, ano do planeta, medido em horas ou anos.
- R → raio médio da órbita de um planeta, medido em quilômetros ou UA.
Isso significa que o cubo do raio médio da órbita do planeta é diretamente proporcional ao quadrado do período de translação do planeta.
Quando estamos comparando dois planetas ou corpos celestes, a fórmula da terceira lei de Kepler se transforma em:
\(\frac{T_1^2}{R_1^3} = \frac{T_2^2}{R_2^3} \)
- T1 e T2 → períodos de revolução de dois planetas.
- R1 e R2 → raios médios das órbitas dos dois planetas em questão.
Na tabela abaixo estão os dados do período e raio médio dos planetas do sistema solar, em que o período e raio médio da Terra são as referências. |1|
|
Planeta |
Período (anos) |
Raio médio (UA) |
|
Mercúrio |
0,241 |
0,38 |
|
Vênus |
0,614 |
0,72 |
|
Terra |
1,000 |
1,000 |
|
Marte |
1,881 |
1,52 |
|
Júpiter |
11,8 |
5,2 |
|
Saturno |
29,5 |
9,2 |
|
Urano |
84,010 |
19,190 |
|
Netuno |
164,800 |
30,060 |
Importante: O UA é a unidade astronômica, ela equivale à distância da Terra ao Sol (1,48 x 108 km).
Veja também: O que diz a segunda lei de Kepler?
Aplicação da terceira Lei de Kepler
A terceira lei de Kepler é um assunto empregado nas áreas de astronomia e astrofísica, além de diversos vestibulares, com o intuito de descobrir os períodos de revolução ou raios médios das orbitas dos corpos celestes. Pensando nisso, selecionamos alguns exemplos de como podemos aplicar a terceira lei de Kepler nas questões.
- Exemplo 1:
Determine o período de revolução aproximado de um planeta X, em anos terrestres, a uma distância de 45 unidades astronômicas do Sol.
Resolução:
Calcularemos o período de revolução do planeta X por meio da fórmula da terceira lei de Kepler:
\(\frac{T_1^2}{R_1^3} = \text{constante} \)
Nesse caso o resultado da lei dos períodos é equivalente a 1.
\(\frac{T^2}{45^3} = 1 \)
\(\frac{T^2}{91125} = 1 \)
\(T^2 = 1 \cdot 91125 \)
\(T^2 = 91125 \)
\(T = \sqrt{91125} \)
\(T \approx 301,9 \, \ \text{anos terrestres}\)
- Exemplo 2:
Existem diversos satélites orbitando a Terra. Supondo que o satélite A tenha raio orbital de 90 mil km e período orbital igual ao período de rotação da Terra, de 24 horas, e o satélite B tenha raio orbital de 50 mil km, calcule o período orbital aproximado do satélite B.
Resolução:
Calcularemos o período orbital do satélite B por meio da fórmula da terceira lei de Kepler, que relaciona dois satélites.
\(\frac{T_1^2}{R_1^3} = \frac{T_2^2}{R_2^3} \)
\(\frac{24^2}{90000^3} = \frac{T_2^2}{50000^3} \)
\(\frac{576}{7,29 \cdot 10^{14}} = \frac{T_2^2}{1,25 \cdot 10^{14}} \)
\(T_2^2 = \frac{576 \cdot 1,25 \cdot 10^{14}}{7,29 \cdot 10^{14}} \)
\(T_2^2 = \frac{576 \cdot 1,25}{7,29} \)
\(T_2^2 = \frac{720}{7,29} \)
\(T_2 \approx \sqrt{98,76} \)
\(T_2 \approx 9,94 \,\ \text{horas} \)
Acesse também: Existe uma quarta lei de Kepler?
Exercícios resolvidos sobre terceira lei de Kepler
Questão 1
(Unicamp - Adaptada) A terceira lei de Kepler diz que “o quadrado do período de revolução de um planeta (tempo gasto para dar uma volta em torno do Sol) dividido pelo cubo da distância média do planeta ao Sol é uma constante.” A distância média da Terra ao Sol é equivalente a 1 UA (unidade astronômica). Entre Marte e Júpiter existe um cinturão de asteroides (vide figura).
Os asteroides são corpos sólidos que teriam sido originados do resíduo de matérias existentes por ocasião da formação do sistema solar.
Se no lugar do cinturão de asteroides essa matéria tivesse se aglutinado formando um planeta, quanto duraria o ano desse planeta em anos terrestres, se sua distância ao Sol for de 2,5 UA?
A) 3,95
B) 3,95
C) 3,95
D) 3,95
E) 3,95
Resolução:
Alternativa E.
Calcularemos o quanto duraria o ano do planeta através da fórmula da terceira lei de Kepler:
\(\frac{T_1^2}{R_1^3} = \frac{T_2^2}{R_2^3} \)
\(\frac{1^2}{1^3} = \frac{T_2^2}{2,5^3} \)
\(\frac{1}{1} = \frac{T_2^2}{15,625} \)
\(15,625 = T_2^2 \)
\(\sqrt{15,625} = T_2^2 \)
\(3,95 \, \ \text{anos terrestres} \approx T_2^2\)
Questão 2
(Faceres) Durante uma aula, um professor de física profere: “O principal discípulo de Tycho Brache, que havia catalogado, durante décadas, as posições de planetas no firmamento, nos revelou que o quadrado do período de translação de um planeta é diretamente proporcional ao cubo do raio médio de sua órbita”.
Um estudante atento pode concluir corretamente que o professor se referia a:
A) Isaac Newton e sua lei de ação e reação.
B) Coulomb e sua lei sobre forças de interação elétrica.
C) Johannes Kepler e sua lei das órbitas, que afirmava estar o Sol no centro de uma elipse.
D) Johannes Kepler e sua terceira lei, chamada de lei dos períodos.
E) Albert Einstein e sua teoria da relatividade.
Resolução:
Alternativa D.
O estudante concluiu corretamente que o professor se referia a Johannes Kepler e sua terceira lei, chamada de lei dos períodos, que fala sobre a relação entre o quadrado do período de translação de um corpo e o cubo do raio médio de sua órbita.
Notas
|1| NUSSENZVEIG, Herch Moysés. Curso de física básica: Fluidos, Oscilações e Ondas, Calor (vol. 2). 5 ed. São Paulo: Editora Blucher, 2015.
Fontes
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Gravitação, Ondas e Termodinâmica (vol. 2). 8. ed. Rio de Janeiro, RJ: LTC, 2009.
NUSSENZVEIG, Herch Moysés. Curso de física básica: Fluidos, Oscilações e Ondas, Calor (vol. 2). 5 ed. São Paulo: Editora Blucher, 2015.