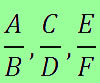Proporção no Enem

Proporção é um tema presente no Enem por ser um conteúdo de grande importância na matemática, pois o trabalho com grandezas é recorrente no cotidiano. Assim, constantemente, deparamo-nos com situações que envolvem grandezas diretamente proporcionais — em que à medida que o valor de uma grandeza aumenta, o da outra também aumenta na mesma proporção — ou grandezas inversamente proporcionais — em que à medida que o valor de uma grandeza aumenta, o da outra diminui na mesma proporção.

No Enem, o conteúdo de proporção é recorrente em questões que abordam a identificação da proporcionalidade, o encontro de valores desconhecidos em situações envolvendo grandezas proporcionais, entre outras situações. Para fazer um bom Enem, é indispensável que se domine a ideia de proporção e seus métodos, como regra de três ou uso de razão.

Leia também: Temas de Matemática que mais caem no Enem

Tópicos deste artigo

• 1 - Resumo sobre proporção no Enem
• 2 - O que é proporção?
  • Grandezas diretamente proporcionais
  • Grandezas inversamente proporcionais
• 3 - Como a proporção é cobrada no Enem?
• 4 - Questões sobre proporção no Enem

Resumo sobre proporção no Enem

• Proporção é um conteúdo bastante recorrente no Enem.

• Duas grandezas podem ser diretamente proporcionais ou inversamente proporcionais.

• Para responder as questões de proporção, é importante dominar, além do conceito, o conteúdo de regra de três e de razão.

O que é proporção?

Vivemos em um mundo cercado de grandezas e medidas, estamos o tempo todo contando, medindo e comparando grandezas. Diante da comparação dessas grandezas, surge a ideia de grandezas proporcionais. Dizemos que duas grandezas são proporcionais quando elas se relacionam de forma proporcional, o que significa que se em determinada situação envolvendo essas duas grandezas, uma delas aumentar o seu valor, a outra também aumentará ou diminuirá na mesma proporção.

Existem dois tipos de proporcionalidade entre as grandezas, elas podem ser diretamente proporcionais ou inversamente proporcionais.

• Grandezas diretamente proporcionais

Duas grandezas são diretamente proporcionais quando, em determinada situação, à medida que uma grandeza aumenta, a outra também aumentará na mesma proporção.

Exemplos:

• A relação entre salário e impostos (quanto maior o seu salário, maior será o desconto líquido de imposto);

• Peso e preço (em itens que compramos pelo peso, quanto maior o peso, maior será o valor pago pelo produto);

• Distância percorrida e tempo (com uma velocidade pré-determinada, quanto maior o tempo, maior será a distância percorrida).

Para que duas grandezas sejam diretamente proporcionais, existe uma relação de proporcionalidade entre elas, isso significa que, por exemplo, se uma grandeza dobrar o seu valor, a outra também dobrará o seu.

• Grandezas inversamente proporcionais

Duas grandezas são inversamente proporcionais se à medida que uma delas aumenta, a outra diminuirá na mesma proporção.

Exemplos:

• Velocidade e tempo (quanto maior a velocidade, menor será o tempo para percorrer determinada distância);

• Vazão e tempo (quanto mais torneiras para encher um tanque ou piscina, menor será o tempo necessário para completar a ação).

Veja também: 3 macetes de Matemática para o Enem

Como a proporção é cobrada no Enem?

Questões que envolvem gradezas são bastante comuns no Enem, e, em alguns casos, trata-se de problemas que envolvem grandezas proporcionais. Os problemas que envolvem proporção podem ser resolvidos, geralmente, utilizando a propriedade fundamental da proporção. Essa propriedade é enunciada também como: o produto dos meios é igual ao produto dos extremos. De forma algébrica, ela é representada assim:

b · c = a · b

As questões que envolvem proporções estão ligadas a problemas cotidianos e podem ser resolvidas com base na propriedade referida e, em alguns casos, na regra de três.

É importante lembrar que a noção de proporcionalidade pode ser cobrada em questões envolvendo razão, geometria plana, entre outras áreas. Vejamos, a seguir, alguns exemplos de questões que envolvem proporção.

Questões sobre proporção no Enem

Questão 1 - (Enem) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas.

Se a mãe ministrou corretamente 30 gotas do remédio a cada 8 horas, então a massa corporal do filho é de

A) 12 kg

B) 16 kg

C) 24 kg

D) 36 kg

E) 75 kg

Resolução
Alternativa A

Sabemos que peso e quantidade de remédio são grandezas proporcionais, já que a dosagem está condicionada ao peso. Montando a razão, temos que 5 gotas está para 2 kg, assim como 30 gotas está para um peso x:

Multiplicando cruzado, temos que:

5x = 60

x = 60 : 5

x = 12 kg

Questão 2 - (Enem) A relação da resistência elétrica com as dimensões do condutor foi estudada por um grupo de cientistas por meio de vários experimentos de eletricidade. Eles verificaram que existe proporcionalidade entre:

• resistência (R) e comprimento (ℓ), dada a mesma secção transversal (A);

• resistência (R) e área da secção transversal (A), dado o mesmo comprimento (ℓ); e

• área da secção transversal (A), dada a mesma resistência (R).

Considerando os resistores como fios, pode-se exemplificar o estudo das grandezas que influem na resistência elétrica utilizando as figuras seguintes.

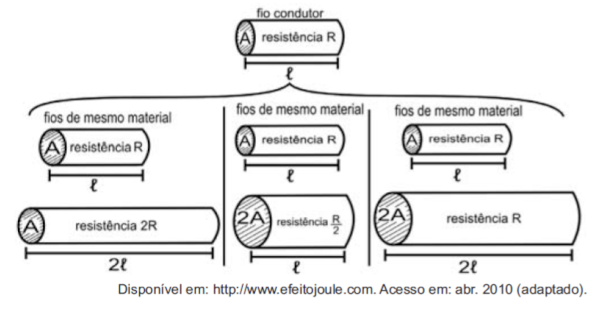
As figuras mostram que as proporcionalidades existentes entre resistência (R) e comprimento (ℓ), resistência (R) e área da secção transversal (A), e entre comprimento (ℓ) e área da secção transversal (A) são, respectivamente:

A) direta, direta e direta.

B) direta, direta e inversa.

C) direta, inversa, direta.

D) inversa, direta e direta.

E) inversa, direta e inversa.

Resolução

Alternativa C

É necessário analisar cada uma das situações:

Na primeira imagem, dobra-se a resistência, quando isso acontece, o comprimento também é dobrado, logo, são grandezas diretamente proporcionais.

Na segunda imagem, ao dobrar-se a área da secção transversal, a resistência se divide por dois, logo, trata-se de grandezas inversamente proporcionais.

Na terceira imagem, ao dobrar-se a área da secção transversal, o comprimento também será dobrado, logo, as grandezas são diretamente proporcionais.

Então a relação entre as grandezas são, respectivamente: direta, inversa, direta.

Crédito da imagem

[1] Gabriel_Ramos / Shutterstock