A geometria espacial é a área da Matemática que estuda a geometria tridimensional, com a compreensão de conceitos importantes, como a análise aprofundada dos sólidos geométricos, dos quais foram desenvolvidas fórmulas para o cálculo do volume e da área total.
No Enem, os conteúdos de geometria espacial são bastante recorrentes, aparecendo questões sobre o tema nas últimas provas. As questões que aparecem no exame vão desde o reconhecimento de sólidos geométricos até as principais propriedades de cada um desses sólidos. São recorrentes também questões que envolvem o volume de sólidos geométricos e o reconhecimento da planificação de um sólido geométrico.
Leia também: Geometria plana no Enem — como esse tema é cobrado?
Tópicos deste artigo
- 1 - Resumo sobre geometria espacial no Enem
- 2 - O que é a geometria espacial?
- 3 - Principais sólidos geométricos estudados na geometria espacial
- 4 - Como a geometria espacial é cobrada no Enem?
- 5 - Questões sobre geometria espacial no Enem
Resumo sobre geometria espacial no Enem
-
A geometria espacial estuda objetos tridimensionais, como os sólidos geométricos.
-
Questões sobre geometria espacial apareceram nas últimas provas.
-
Os conteúdos da geometria espacial que caem na prova são:
-
reconhecimento de sólidos geométricos;
-
cálculo de área total e volume de sólidos geométricos;
-
propriedades específicas dos sólidos geométricos;
-
planificação.
-
O que é a geometria espacial?
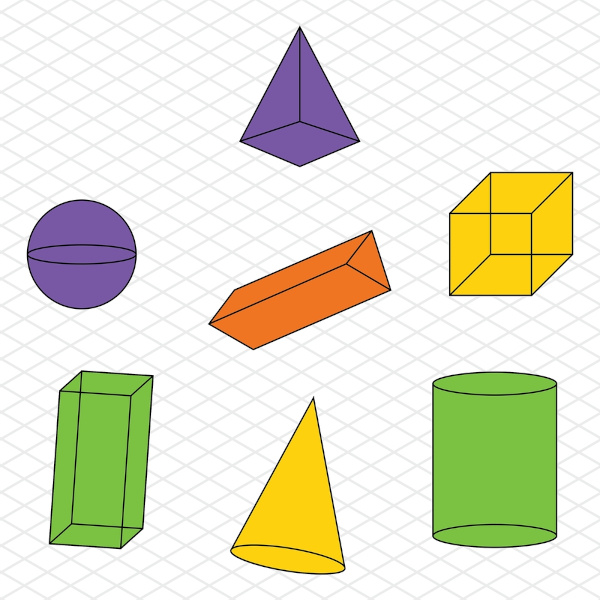
A geometria espacial é a área da Matemática que estuda objetos geométricos tridimensionais. Estamos cercados de formas geométricas, como o cone, a esfera, os prismas, entre outras, e conhecer cada uma delas é fundamental.
Na geometria espacial, são estudados os sólidos geométricos, divididos em dois grupos:
Os poliedros são classificados como prismas, pirâmides e outros. Já os corpos redondos ou sólidos de revolução mais comuns são: o cone, o cilindro e a esfera. Além de reconhecer esses sólidos geométricos, é importante saber as características de cada um deles e a sua planificação. É na geometria espacial que se estuda também a área total e o volume de um sólido geométrico. Veja, a seguir, os principais sólidos geométricos e a fórmula de cada um para o cálculo de sua área total e seu volume.
Leia também: Dicas de Matemática para o Enem
Principais sólidos geométricos estudados na geometria espacial
-
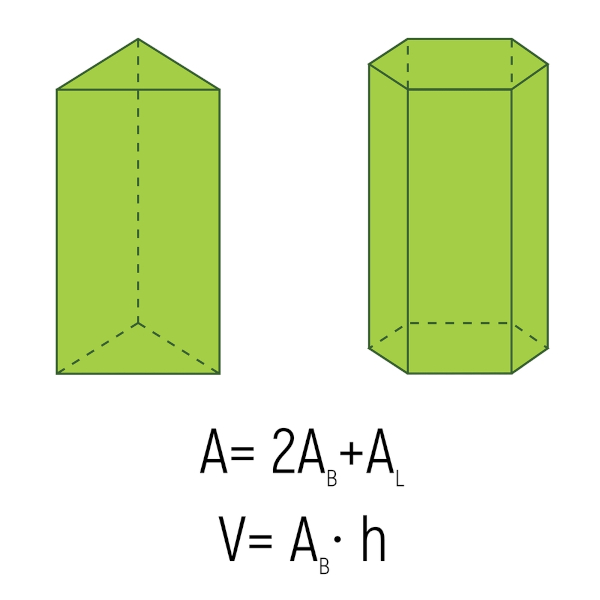
Prismas
O prisma é o sólido geométrico formado por duas bases congruentes que sejam polígonos quaisquer, e possui laterais formadas por paralelogramos, unindo as duas bases. Existem vários tipos de prima, como o prisma de base hexagonal, o prisma de base triangular, o prisma de base quadrada, entre outros.
-
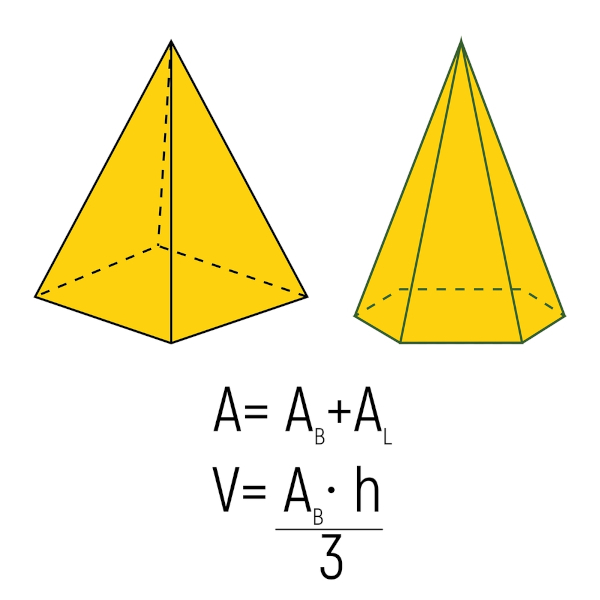
Pirâmides
A pirâmide é um sólido geométrico que tem uma base formada por um polígono qualquer e faces laterais formadas por triângulos, encontrando-se num ponto em comum conhecido como vértice da pirâmide.
Assim como os prismas, a pirâmide pode ter várias bases diferentes, como a pirâmide de base quadrada, a pirâmide de base pentagonal, a pirâmide de base hexagonal, entre outras.
-
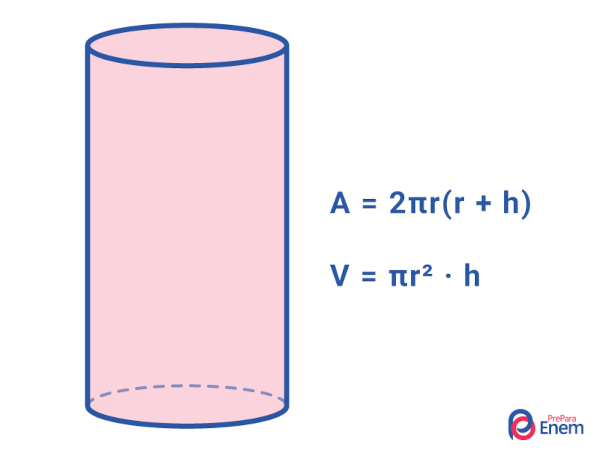
Cilindro
O cilindro é um corpo redondo que possui duas bases formadas por círculos de mesmo raio. Para calcular o seu volume, precisamos do valor do seu raio e da sua altura. Em corpos redondos, é bastante comum a utilização da constante π para cálculo de volume e de área total.
-
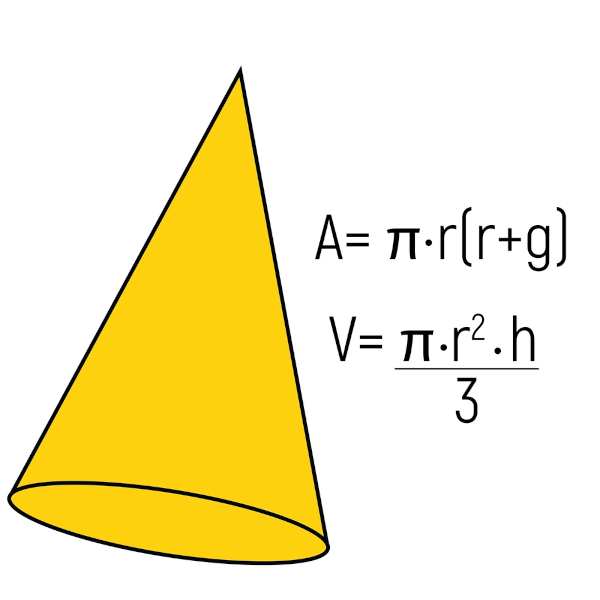
Cone
O cone é outro corpo redondo, pois ele é o sólido geométrico formado pela rotação de um triângulo. Assim como a pirâmide, o cone possui um vértice, mas, no caso, a base do cone é sempre um círculo.
A distância de um ponto da circunferência da base até o vértice é conhecida como geratriz, representada na fórmula da área total por g. Além da geratriz, da altura e do raio da base, no cone também é necessário utilizar a constante π para calcular o volume e a área.
-
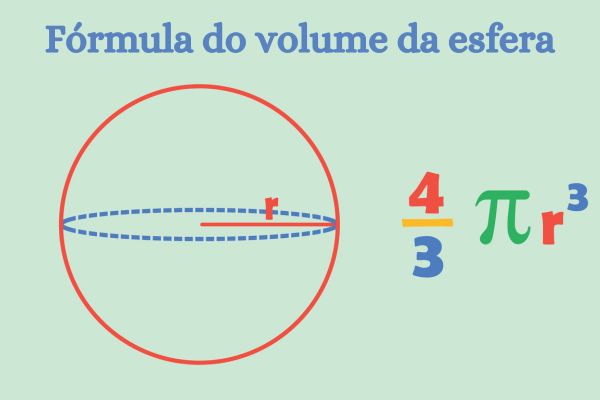
Esfera
O último corpo redondo é a esfera, uma forma bastante cotidiana. Ela é o conjunto de pontos que estão a uma mesma distância de um centro no espaço. Essa distância é conhecida como raio, que utilizamos para calcular o seu volume e sua área total.
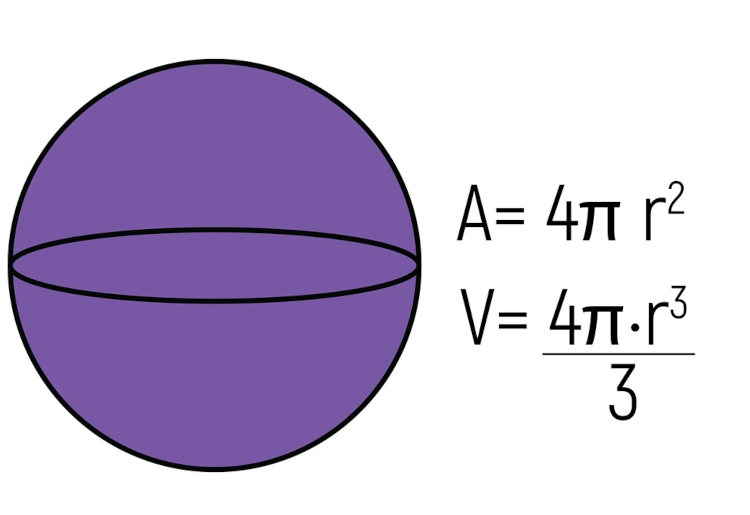
Como a geometria espacial é cobrada no Enem?
Nos últimos exames, houve questões envolvendo geometria espacial. O tema mais recorrente nas provas ligado à geometria espacial é o cálculo do volume de sólidos geométricos. Além do cálculo de volume, é comum que haja questões sobre a identificação de sólidos geométricos, suas características e propriedades. Então, para resolver a prova, é fundamental que se saiba identificar as características de figuras espaciais bem como resolver situações-problemas que envolvam conhecimento geométrico de espaço e forma.
Existem também algumas questões do Enem que cobram a projeção de objetos tridimensionais no plano, o que exige do candidato que ele consiga relacionar a geometria plana com a geometria espacial. A planificação desses sólidos geométricos também já apareceu em algumas questões da prova.
Então, para se sair bem nas questões de geometria espacial, é importante que você conheça bem cada um dos sólidos geométricos, suas características e propriedades, e é fundamental que se domine o cálculo de volume e de área total de cada um desses sólidos.
As questões sobre a geometria espacial quase sempre vêm bem contextualizadas, com situações-problemas que devem ser resolvidas com base no conhecimento geométrico sobre aquele sólido. Assim, é fundamental a realização de uma leitura minuciosa da questão, pois entender o problema é imprescindível para alcançar sua resolução.
Leia também: Temas de Matemática que mais caem no Enem
Questões sobre geometria espacial no Enem
Questão 1
(Enem) Maria quer inovar sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas está a planificação dessas caixas.
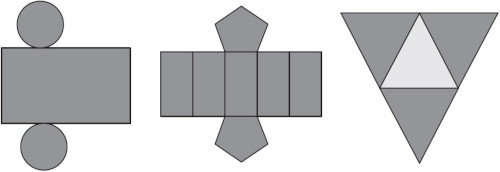
Quais serão os sólidos geométricos que Maria obterá com base na planificação?
A) Cilindro, prima de base pentagonal e pirâmide.
B) Cone, prisma de base pentagonal e pirâmide.
C) Cone, tronco de pirâmide e pirâmide.
D) Cilindro, tronco de pirâmide e prisma.
E) Cilindro, prisma e tronco de cone.
Resolução:
Alternativa A
Analisando a primeira planificação, é possível identificar que se trata de um cilindro, pois note que ela possui duas faces circulares e a face lateral é um único retângulo.
Analisando a segunda planificação, é possível identificar que se trata de um prisma (note que ele possui base pentagonal), pois tem duas faces pentagonais e cinco faces retangulares.
Por fim, a terceira planificação é uma pirâmide de base triangular. Perceba que ela possui uma base triangular ao meio e outras três faces triangulares, que formam as laterais.
Então as planificações são, respectivamente, um cilindro, um prisma de base pentagonal e uma pirâmide.
Questão 2
(Enem 2014) Uma pessoa comprou um aquário em forma de um paralelepípedo retângulo reto, com 40 cm de comprimento, 15 cm de largura e 20 cm de altura. Chegando em casa, colocou no aquário uma quantidade de água igual à metade de sua capacidade. A seguir, para enfeitá-lo, colocará pedrinhas coloridas, de volume igual a 50 cm³ cada, que ficarão totalmente submersas no aquário.
Após a colocação das pedrinhas, o nível da água deverá ficar a 6 cm do topo do aquário. O número de pedrinhas a serem colocadas deve ser igual a
A) 48.
B) 72.
C) 84.
D) 120.
E) 168.
Resolução:
Alternativa A
Para encontrar o volume desejado, basta lembrar que o volume da pedrinha será igual ao volume que aumentou no líquido. Como tem água até a metade da capacidade do aquário, e pedrinhas, sabemos que a metade de 20 é 10, e que (desses 10 cm, nesse caso) 10 – 6 = 4 cm. Dessa forma, a altura da água aumentou 4 cm quando se acrescentou as pedrinhas. Então, basta calcular o volume com a altura igual a 4 cm.
V = 40 ⸳ 15 ⸳ 4 = 2400 cm³
Como cada pedrinha possui 50 cm³de volume, então temos que:
2400 : 50 = 48 pedrinhas