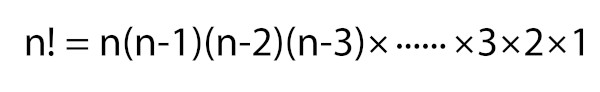Análise combinatória no Enem

Análise combinatória é um conteúdo bastante recorrente no Enem, que costuma cobrar desde o princípio multiplicativo, conhecido também como princípio fundamental da contagem, até os agrupamentos (permutação, combinação e arranjo). A análise combinatória é a área da Matemática que tem como objetivo contar o número de reagrupamentos possíveis para determinadas situações. É bastante comum ver aplicações desse tema no nosso dia a dia, como em jogos de loteria ou no estudo das probabilidades, genética, entre outras aplicações.

Leia também: Temas de Matemática que mais caem no Enem

Tópicos deste artigo

• 1 - Como a análise combinatória é cobrada no Enem?
• 2 - O que é análise combinatória?
• 3 - Questões sobre análise combinatória no Enem

Como a análise combinatória é cobrada no Enem?

A análise combinatória é um conteúdo bastante recorrente na prova do Enem. Em todos os anos, desde 2009, aparece pelo menos uma questão que pede algum dos tipos de agrupamentos ou a aplicação do princípio fundamental da contagem.

O interessante das questões que envolvem esse assunto é que, na grande maioria delas, é exigida boa interpretação do candidato. A dificuldade em resolvê-las, na maioria das vezes, está ligada mais à interpretação do problema do que ao cálculo da quantidade de agrupamentos em si. Então, para se dar bem, é importante não só que o candidato domine a conta, que é basicamente simples, mas que ele consiga aplicá-la em situações-problemas bem elaboradas. A análise combinatória exige muita atenção para os enunciados das questões e saber interpretá-las.

No Enem é comum que, além do princípio fundamental, apareçam questões envolvendo os agrupamentos, sendo os mais recorrentes a combinação e o arranjo. Compreender a diferença entre os dois é fundamental para acertar as questões e também é necessário conhecer as fórmulas de ambos.

Muitas questões do Enem só pedem para você indicar na fórmula como seria calculada a combinação ou o arranjo. Quase sempre não é necessário calcular o valor do agrupamento em si, mas apenas indicá-lo substituindo os valores na fórmula.

Então, em resumo, para se preparar bem para as questões de análise combinatória do Enem, busque:

• treinar resolvendo as questões sobre o tema dos anos anteriores para desenvolver sua interpretação de texto;
• aprender a diferença entre os tipos de agrupamentos;
• conhecer as fórmulas de cada um dos agrupamentos;
• saber analisar as alternativas, pois quase sempre não é necessário realizar o cálculo da combinação ou do arranjo em si.

Veja também: Dicas de Matemática para o Enem

O que é análise combinatória?

Análise combinatória é a área da Matemática que auxilia na contagem e na análise de todos os reagrupamentos possíveis dentro de um conjunto de elementos. Nessa área, são utilizadas  ferramentas para a resolução de diferentes situações que envolvem agrupamentos, surgindo o princípio fundamental da contagem, conhecido também como princípio multiplicativo.

O princípio fundamental da contagem afirma que, se duas ou mais decisões serão tomadas simultaneamente, então a quantidade de maneiras distintas que essas decisões poderão ser tomadas pode ser calculada pelo produto entre a quantidade de possibilidades de cada uma delas, ou seja, se se existem n decisões a serem tomadas {d_1, d₂, d₃ d₄ … d_n} e cada uma delas pode ser tomada de {m₁, m₂, m₃, m₄, … m_n} maneiras, então o número de maneiras que essas decisões poder ser tomadas simultaneamente é calculado por:  m₁· m₂· m₃· m₄· …·m_n.

Utilizando o princípio fundamental da contagem, são desenvolvidos outros conceitos importantes na análise combinatória, como a permutação. Conhecemos como permutação todas os conjuntos ordenados que podemos formar com todos os elementos de um conjunto. Para calcular a permutação, utilizamos a fórmula:

P_n = n!

Vale dizer que n! (lê-se n fatorial) é a multiplicação de n por todos os seus antecessores.

Outros dois agrupamentos são as combinações e os arranjos. Ambos possuem fórmulas específicas desenvolvidas a partir do princípio fundamental da contagem. Arranjo é a quantidade de agrupamentos ordenados que podemos montar com p elementos de um conjunto que possui n elementos e é calculado por:

A combinação é a quantidade de subconjuntos possíveis que podemos montar com p elementos de um conjunto de n elementos. É muito importante diferenciar arranjo de combinação, pois, no arranjo, a ordem é importante, mas, na combinação, não. Para calcular a combinação, utilizamos a fórmula:

Questões sobre análise combinatória no Enem

Questão 1 – (Enem 2012) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.

Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.

O diretor sabe que algum aluno acertará a resposta porque há:

A) 10 alunos a mais do que possíveis respostas distintas.
B) 20 alunos a mais do que possíveis respostas distintas.
C) 119 alunos a mais do que possíveis respostas distintas.
D) 260 alunos a mais do que possíveis respostas distintas.
E) 270 alunos a mais do que possíveis respostas distintas.

Resolução

Alternativa A.

Pelo princípio multiplicativo, basta encontrar o produto das decisões a serem tomadas:

• 5 objetos;
• 6 personagens;
• 9 cômodos;

5· 6 · 9 = 270

Como há 280 alunos, então 280 – 270 = 10 → Há 10 alunos a mais do que as possíveis respostas distintas.

Questão 2 – (Enem 2016) O tênis é um esporte em que a estratégia de jogo a ser adotada depende, dentre outros fatores, de o adversário ser canhoto ou destro.

Um clube tem um grupo de 10 tenistas, sendo que 4 são canhotos e 6 são destros. O técnico do clube deseja realizar uma partida de exibição entre dois desses jogadores, porém não poderão ser ambos canhotos. Qual o número de possibilidades de escolha dos tenistas para a partida de exibição?

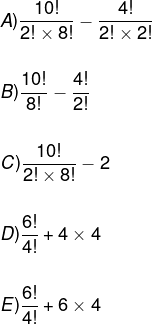
Resolução

Alternativa A.

Antes de qualquer coisa, sempre precisamos compreender se estamos lidando com combinação ou arranjo. Note que, nesse caso, a ordem não é importante, pois a partida entre os jogadores A e B seria a mesma caso fosse entre os jogadores B e A. Como a ordem não importa, estamos trabalhando com uma combinação.

Queremos indicar como seria calculado o total de partidas em que ambos os jogadores não fossem canhotos. Para isso calcularemos a diferença entre o total de partidas possíveis e o total de partidas realizadas entre dois canhotos.

Como há 10 jogadores e serão escolhidos 2, então é uma combinação de 10 elementos tomados de 2 em 2, ou seja, C_10,2 partidas possíveis.

Já a quantidade de partidas em que os dois jogadores são canhotos — como há 4 canhotos e vamos escolher 2 — é calculada por C_4,2.

Calculando a diferença, temos:

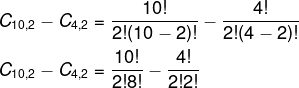
Note que não é necessário realizar os cálculos das combinações, pois já encontramos a alternativa correspondente.